ライトフレームとダークフレームどっちを増やす？ (追記あり)

2021/4/3追記: 以下の計算には誤りがあると思われます。詳細は記事末の追記を参照してください。

天体写真をコンポジット処理するのはランダムなノイズを減らすためです。重ねるライトフレームの枚数が多いほどノイズが減ります。

一方ダーク減算は固定パターンのノイズを除去する一方でランダムなノイズを増やします。ノイズの増加を抑制するためにはダークフレームを複数枚をコンポジット処理したものを使って減算します。

ライトフレームもダークフレームもどちらも増やせば増やすほどノイズは減るのですが、限られた撮影時間の中でどちらを増やすのが得でしょうか？僕は日頃ライトフレーム 8 枚、ダークフレーム 4 枚でコンポジットしているのですが、あと 4 枚増やすとしたらどちらを増やせばよいでしょう？

先日撮影した M101 の写真、カブリが大きくてボツにしたのも含めてライトフレームを 12 枚用意、ダークフレームは 4 枚しか撮っていませんが別の日に撮ったものを合わせて 8 枚用意して、ライト 8 枚 + ダーク 8 枚のコンポジットと、ライト 12 枚 + ダーク 4 枚のコンポジットを実施して、ライト 8 枚 + ダーク 4枚の写真と比較してみました。それぞれ DeepSkyStacker の出力を同じトーンカーブで処理しただけの画像です。

https://rna.sakura.ne.jp/share/light-or-dark/L8+D8-vs-L12+D4.jpg

ライトフレームを増やした方はノイズが減っているのがわかりますが、ダークを増やした方はほとんど変わらないような？ 4 枚から 8 枚で倍に増やしたので結構効果があるかと思ったのですが。気温の違う日のダークじゃだめ？

よくわからないので基本的なところから計算してみました。以下ではダークノイズだけ考えます。

標準偏差と分散

ライトフレームの各ピクセル値はシグナルとノイズの和です。ノイズが乗っているのでシグナルの値が同じ大きさのピクセルでも場所によってピクセル値がばらついて、フラットなはずの画像がザラザラして見えます。

シグナル値がどのピクセルでも等しいフラットな画像を考えます。ピクセル値を変数 $x$ で表すと、含まれるノイズの平均的な大きさはその標準偏差 $D(x)$ で、分散 $V(x)$ はその 2 乗です。

分散には以下の性質があります( $a$ は定数)。

$V(ax) = a^{2}V(x)$	(1)
$V(x + a) = V(x)$	(2)
$V(x + y) = V(x) + V(y)$	(3)*1

これらの公式を使って画像処理後のノイズを計算します。

ライトフレームのコンポジットによるノイズの低減

ライトフレーム $i$ のピクセル値を $x_i$ とすると、 $N$ 枚を加算平均コンポジットした結果のピクセル値の分散 $V(x')$ は、公式 (1), (3) から、

$V(x') = V(\frac{x_1 + x_2 + x_3 +\cdots}{N}) = \frac{V(x_1) + V(x_2) + V(x_3) + \cdots}{N^2}$

各フレームの分散が同じ値 $V(x)$ だとすると、

$V(x') = \frac{N V(x)}{N^{2}} = \frac{V(x)}{N}$

となります。ノイズの大きさ = 標準偏差はこの平方根なので、

$D(x') = \frac{1}{\sqrt{N}} D(x)$

つまり、元のノイズの大きさ $D(x)$ と比べてコンポジット処理後ノイズの大きさは、ライトフレームの数の平方根分の 1 になります。4 枚なら $\frac{1}{2}$ 、16 枚なら $\frac{1}{4}$ です。

ダーク減算によるノイズの増加

ダーク減算を行うとノイズが増えてしまいます。これはノイズの差の分散はノイズの分散の和になってしまうためです。ダーク減算後の分散 $V(x - x_{dark})$ は公式 (1), (3) から、

$V(x - x_{dark}) = V(x + (-1)x_{dark}) = V(x) + (-1)^{2} V(x_{dark}) = V(x) + V(x_{dark})$

ピクセル値 $x$ をシグナル成分 $x_{signal}$ とノイズ成分 $x_{noise}$ に分けると、

$V(x) = V(x_{signal} + x_{noise}) = V(x_{signal}) + V(x_{noise})$

ここではシグナル値は一定なので $x_{signal}$ は定数であり、公式 (2) より

$V(x) = V(x_{noise})$

$V(x_{noise})$ はダークフレームのピクセル値の分散 $V(x_{dark})$ と等しいと考えられます。よって、

$V(x) = V(x_{dark})$
$V(x - x_{dark}) = V(x) + V(x) = 2 V(x)$
$D(x - x_{dark}) = \sqrt{2} D(x)$

つまり、ダーク減算後のノイズの大きさは $\sqrt{2}$ = 約 1.41 倍に増えてしまいます。

この効果はダークフレームをコンポジットしてから減算すると緩和されます。ダークフレームを $M$ 枚用意してコンポジットした画像のピクセル値を $x_{dark}'$ とすると、その分散 $V(x_{dark}')$ は先ほどのコンポジット処理結果の分散の計算から、

$V(x_{dark}') = \frac{V(x_{dark})}{M}$

よって、

$V(x - x_{dark}') = V(x) + V(x_{dark}') = (1 + \frac{1}{M}) V(x)$
$D(x - x_{dark}') = \sqrt{1 + \frac{1}{M}} D(x)$

つまり、1.41 倍だったノイズ増加は、ダークフレーム 2 枚なら 1.22 倍、4 枚で 1.12 倍、8 枚で 1.06 倍にまで抑えられます。

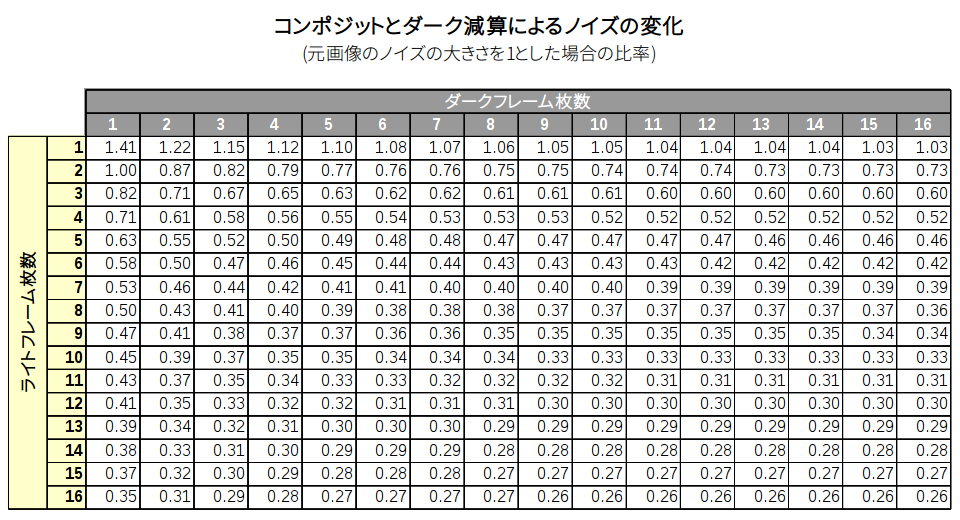
コンポジットとダーク減算によるノイズの変化

ライトフレーム $N$ 枚を、それぞれダークフレーム $M$ 枚のコンポジット結果でダーク減算してからコンポジットした結果のピクセル値を $x''$ とすると、分散 $V(x'')$ は、

$V(x'') = V(\frac{(x_1 - x_{dark}') + (x_2 - x_{dark}') + \cdots}{N})$
$= \frac{V(x - x_{dark}')}{N}$
$= \frac{1 + \frac{1}{M}}{N} V(x)$
$= (\frac{1}{N} + \frac{1}{MN}) V(x)$
$D(x'') = \sqrt{\frac{1}{N} + \frac{1}{MN}} D(x)$

うーん、これでいいのかな？

そんなわけで、 $N$ と $M$ の組み合わせによって、元画像のノイズに比べて処理後のノイズがどう変化するかを表にしてみました。

https://rna.sakura.ne.jp/share/light-or-dark/composite-and-dark-subtract-table.png

ライト 8 枚 + ダーク 4 枚のノイズは 0.40 、ライト 8 枚 + ダーク 8 枚のノイズは 0.38 で 5% しか違いません。一方、ライト 12 枚 + ダーク 4 枚のノイズは 0.32 で、25% の違いがあります。やはりライトフレームを増やした方がノイズが減るようです。

以上はセンサーのダークノイズだけを考慮したものですが、ライトフレームのコンポジットはフォトンノイズ(被写体から届く光子の数そのもの統計的揺らぎによるノイズ)にも効くので、そういう意味でもライトフレームを増やすほうがお得なはず。

参考

コンポジットとダーク減算の計算は、田中光学工業株式会社の記事「ノイズの計算」を参考にしました。ダーク減算でノイズが増えるというのもこの記事で知りました。

分散の公式はすっかり忘れてしまっていたので、高校数学の美しい物語の記事「期待値と分散に関する公式一覧」を参照しました。

2021/4/3 追記: 本記事の計算の誤りについて

冒頭でお伝えしたように上の計算には誤りがあるものと思われます。というのは、ダーク減算後のフレームのコンポジットのノイズの計算で、各フレームに含まれるマスターダーク減算由来のノイズがフレーム間で相関することを考慮に入れていないからです。

$V(x'') = V(\frac{(x_1 - x_{dark}') + (x_2 - x_{dark}') + \cdots}{N})$
$= \frac{V(x - x_{dark}')}{N}$

1行目から2行目への式変形では「ライトフレームのコンポジットによるノイズの低減」で導出したコンポジット後のピクセル値の分散の式 $V(x') = \frac{V(x)}{N}$ を利用しているのですが、この式の導出で公式 (3) ( $V(x + y) = V(x) + V(y)$ )を使っていました。

公式 (3) は注釈にあるように「x と y が無相関」であることを前提としています。しかし、ダーク減算後のフレームのコンポジットでは全てのフレームで同じマスターダークを減算しているため、マスターダークに由来するノイズ成分は相関するはずです。

マスターダーク由来のノイズ成分は、コンポジットの際にアライメントを行わないならば全フレームで完全に一致するので何枚コンポジットしようと全く減りません。ガイドエラーがありアライメントを行うなら全フレームは一致しませんが、いくらかは相関が残るものと考えられます。

この点は Twitter であぷらなーとさんにご指摘いただきました。

私も見直し中です。
ライトからダークを引くと、ダーク中のランダムノイズがライト中の固定ノイズに化けてしまうので、以後（ライトーダークを）コンポジットしても「その成分（元々ダーク中に存在していたノイズ）」は不変である、という仮定の下での推論なので、私が勘違いしてるかもです。
— あぷらなーと (@PG1wvzio4yvwFXW) March 31, 2021